开课教师

游道建

开课班级

17学前（2）

开课时间

2018年12 月28日

星期五第2节

设计思路

根据教学大纲要求本节课教学侧重揭示概念的深刻内涵，要进行正反两方面的分析论证，重点分析思路，抓住这一有利时机使学生学会严谨科学的分类讨论方法，培养学生全面、系统、辩证、周密地分析问题、讨论问题的能力，特别要培养学生逻辑思维能力，同时培养学生辩证唯物主义观点；强调几种形式互化时要向学生充分揭示各种形式的特点和几何特征等，使学生明白为什么要转化，并加深对各种的理解。

教学分析

教材

分析

本节是在学习直线的点斜式，斜截式的基础上引导学生认识他们的实质，即都是二元一次方程，从而对直线与二元一次方程的关系进行探究，进而得出直线的一般式方程，这也为下节课的学习做好准备。

学情

分析

职专学生抽象思维的能力比较欠缺，本节课对学生的分析能力和分类讨论能力有一定要求，特别是用分类讨论思想来解决问题的能力，学生学习起来有一定难度，所以需要老师逐渐的引导。

教学条件分析

利用ppT并结合知识点的纲要板书，节省时间，同时让学生能随时看到主要知识点，提高教学效果。

教学目标

通过本堂课的学习，明白直线与二元一次方程之间的关系，掌握直线的一般式方程以及明确它的形式特征。

通过探究直线与二元一次方程的关系，让学生积极、主动地参与观察，分析、归纳、进而得出直线的一般式方程，培养学生勇于探究的精神和学会用分类讨论的数学思想方法解决问题

教学重点

理解直线与二元一次方程的关系，直线的一般式方程

教学难点

理解直线的一般式方程及直线与二元一次方程一一对应的关系

教法

分类讨论、讲练结合教学法

学法

在教师的引导下让学生积极、主动参与观察，分析、归纳、分类

讨论学习。

创设

情景

兴趣

导入

（5分钟）

(1) 复习:引导学生回顾前面学过的直线方程的几种不同形式。  

直线方程 形式 ：

点斜式:   

斜截式:   

（2）提问:从上述两种形式的直线方程中，大家能否找到它们的共同特点呢?(都是关于x，y的二元一次方程)

学生

思考

PPT

提出问题，激发学习兴 趣

探索

新知，理解概念（15分钟）

问题1:平面直角坐标系中的每一条直线都可以用一个关于x，y的二元一次方程表示吗?

在平面直角坐标系中，每一条直线在斜率k存在和k不存   在两种情况下，直线方程可分别写为y=kx+b和x=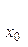两种形式。我们来判断它们是不是一个关于x，y的二元一次方程，即:方程Ax+By+C=0(A、B不同时为0)  

结论:在平面直角坐标系中，任意一条直线都可以用二元一次方程Ax+By+C=0(A、B不同时为0)来表示。  

问题2:每一个关于x,y的二元一次方程都表示一条直线吗?

对任意一个二元一次方程Ax+By+C=0(A、B不全为0)，把它变形，看他能否化成直线方程的某一种形式。  

（1）B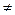0时，方程化为  y=-(A/B)x-C/B   (斜截式方程)

（2）B=0时，由于A、B不同时为0，所以A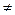0，此时方程可化为x=-(C/A) ，

它表示为与Y轴平行（当C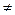0时）或重合（当C=0时）的直线。        

 结论:每一个二元一次方程都表示平面上的一条直线。

通过问题1，2的思考，最终我们得出了平面直角坐标系中，直线与二元一次方程的关系

3）.探究发现

由上可知，关于x，y的二元一次方程，它都表示一条直线。  

我们把关于x，y的二元一次方程  

Ax + By + C=0   (其中A,B不全为0)叫做直线的一般式方程。

一般式方程有如下的规定:

(1)一般按含项x、含项y、常数项顺序排列;  

(2)x项的系数为正;

(3)x，y的系数和常数项一般不出现分数;

学生

理解直线与二元一次方程的关 系

PPT

传 授

学 生

如何理解、分析、讨论相关概念之间联系

巩固

知识

典型

例题

（10分钟）

例1 将方程化为直线的一般式方程，并分别求出该直线在x轴与y轴上的截距．

解 ：   由     得

                   x-2y+5=0

这就是直线的一般式方程．在方程中令，则x=-5，故直线在x轴上的截距为-5；令，则y=  ，故直线在y轴上的截距为    ．

例2  已知直线经过点A（6，- 4），斜率为– 4/3，求直线的点斜式和一般式方程.

解：经过点A（6，- 4）并且斜率等于- 4/3 的直线方程的点斜式是          

              y   + 4 = -4/3 （x – 6）

化成一般式，得         4x+3y–12=0 

例3  把直线L的方程x –2y+6= 0化成斜截式，求出直线L的斜率和它在x轴与y轴上的截距.

解：将原方程移项，得2y =   x+6，                    

        两边除以2，得斜截式   y=x+3

因此，直线L的斜率k=1/2，它在y轴上的截距是3 ；令y=0，可得  x= -6即直线L在x轴上的截距是- 6 。

学生思考，解答问题

PPT

通过例题

进一步理解概念，巩固知识

运用

知识

强化

练习

（10分钟）

1．将下列直线方程化为一般方程：

（1）；          

（2）．

2. 求直线x-2y+8=0在x轴、y轴上的截距及直线的斜率。

思考

求解

PPT

了解学生知识掌握的情况

归纳

小结（ 5分钟）

直线的一般式方程

结论：方程（其中A、B不全为零） 叫做直线的一般式方程．

回 顾

PPT

再次理解新知

作业

布置

教材P59   习题8.2  A组 6.

板书

设计

课题名称

（知识要点）            教学过程分析            学生练习：

 1.                                            1、甲学生        2、乙学生

2.                       课件展示

3.

教学

反思

数学教学过程中，常用的数学思想方法很多，转化的思想，类比归纳与类比联想的思想，分类讨论的思想，数形结合的思想以及配方法、换元法、待定系数法、反证法等等。这些基本思想和方法分散地渗透在数学教材的各章节之中。在平时的教学中，教师要在传授基础知识的同时，有意识地、恰当地讲解与渗透基本数学思想和方法，帮助学生掌握科学的方法，从而达到传授知识，培养能力的目的，只有这样，学生才能灵活运用和综合运用所学知识。而我本堂课主要渗透了分类讨论及数形结合的数学思想。